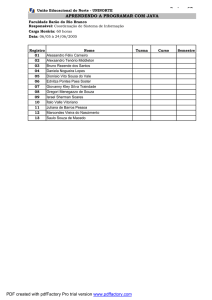
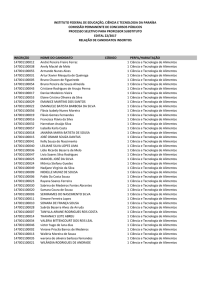
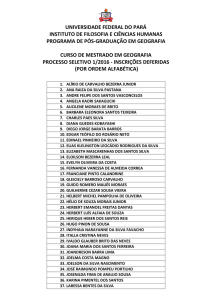
E.E. Dona Antônia Valadares
MATEMÁTICA
1º ANO
TEORIA DOS CONJUNTOS
PROFESSOR: ALEXSANDRO DE SOUSA
http://donaantoniavaladares.comunidades.net
Conjuntos:
Não existe uma definição formalizada do que vem a ser um
conjunto. O que temos é uma ideia ou uma noção do que
vem a ser um conjunto.
De uma maneira geral, temos que um conjunto é tudo aquilo
que nos dá uma ideia de lista,coleção, agrupamento ou
classe de objetos bem definidos
Objetos: Qualquer coisa: números, pessoas, letras, rios, etc... .
Elementos ou membros de um conjunto
Prof: Alexsandro de Sousa
Exemplo
1. Os números 1, 3, 7 e 10
2. As vogais do alfabeto: a, e, i, o e u
3. As pessoas que habitam a Terra
4. Os alunos que faltaram à aula
5. Os times de futebol do estado de Minas Gerais
6. Os números 2, 4, 6, 8, ...
Prof: Alexsandro de Sousa
Conjunto dos times de futebol para os quais os alunos
de uma classe torcem:
Brasiliense, Gama, Ceilândia finito
Conjunto dos dias em que uma pessoa pratica natação:
segunda-feira, quarta-feira, sexta-feira finito
Conjunto dos números pares:
0, 2, 4, 6, 8... infinito
Prof: Alexsandro de Sousa
Prof. Alexsandro de Sousa
Notação:
Conjuntos: Letras maiúsculas: A, B, X, Y, ...
Elementos: Letras minúsculas: a, b, c, d ...
Por Extensão, Tabular ou Enumerativa:
Descrição pela citação dos elementos:
Por Propriedade Característica:
A = { x I x é uma pessoa que habita a Terra }
Representamos o conjunto
através de uma propriedade B = { x I x é um rio do Brasil }
característica de seus
X = { x I x é um número primo positivo }
elementos.
Prof: Alexsandro de Sousa
V {x x é vogal}
S {x R 5x 10 0}
Diagrama de Euler - Venn:
A
a e i
o u
B
1 3 7
10
Prof: Alexsandro de Sousa
Para indicar que um elemento pertenece a um
conjunto se usa o símbolo:
Se um elemento não pertenece a um conjunto se
usa o símbolo:
Exemplo:
Seja M = {2; 4; 6; 8; 10}
2 M ... se lê 2 pertenece ao conjunto M
5 M ... se lê 5 não pertenece ao conjunto M
Prof: Alexsandro de Sousa
A
b A
e A
w A
a
• a pertence ao conjunto A
• b NÃO pertence ao conjunto A
X
8 X
13 X
1 X
2
X = { x I x é um número primo positivo }
1 Não é um número primo
Prof: Alexsandro de Sousa
CONJUNTO VAZIO: É um conjunto que não tem
elementos, também se chama conjunto nulo.
Geralmente se representa pelos símbolos: ou { }
A = ou A = { } se lê: “A é o conjunto vazio” ou “A
é o conjunto nulo “
Exemplos:
M = { números maiores que 9 e menores que 5 }
P={x/
1
0}
X
Prof: Alexsandro de Sousa
CONJUNTO UNITÁRIO É o conjunto que tem um só
elemento.
Exemplos:
2
x
/
x
4 x 0
F = { x / 2x + 6 = 0 };
G=
CONJUNTO FINITO É o conjunto com limitado
número de elementos.
Exemplos:
E = { x / x é um número impar positivo menor que 10 }
N = { x / x2 = 4 }
Prof: Alexsandro de Sousa
CONJUNTO INFINITO
É o conjunto com ilimitado número de elementos.
Exemplos: R = { x / x < 6 }
S = { x / x é um número par }
CONJUNTO UNIVERSAL
É um conjunto referencial que contém todos os
elementos de uma situação particular, geralmente
se representa pela letra U
Exemplo:
de todos os números é o conjunto dos NÚMEROS
COMPLEXOS.
Prof: Alexsandro de Sousa
INCLUSÃO
Um conjunto A está incluso em outro conjunto B, se e
somente se, todo elemento de A for também elemento
de B.
NOTAÇÃO : A
B
Se lê : A está incluso em B, A é subconjunto de B, A
está contido em B , A é parte de B.
REPRESENTAÇÃO GRÁFICA :
B
Prof: Alexsandro de Sousa
A
PROPRIEDADES:
I) Todo conjunto está incluido em si mesmo. A A
II) O conjunto vazio se considera incluido em
qualquer conjunto. A
III) A está incluido em B ( A B ) equivale a dizer
que B contém A ( B A )
IV) Se A não está incluido em B ou A não é
subconjunto de B significa que pelo menos um
elemento de A não pertence a B. ( A B )
V) Simbolicamente: A B x A x B
Prof: Alexsandro de Sousa
• Conjuntos Iguais :
Dois conjuntos são iguais se, e somente se, possuem os
mesmos elementos
Ex: A = { a, b, c, d, e }
B = { a, b, c, d, e }
A=B
A = { 1, 2, 3, 4 }
B = { 3, 1, 4, 2 }
A=B
C = { 5, 6, 5, 7 }
D = { 7, 5, 7, 6 }
C=D
•A
1 5 9
7 10
Prof: Alexsandro de Sousa
B
1 5 8
7 10
A≠B
•Subconjuntos :
A é subconjunto de B se cada elemento do
conjunto A é também elemento do conjunto B .
A é subconjunto de B
U
B
9
7 A 1
10
Prof: Alexsandro de Sousa
A é subconjunto de B
5
A está contido em B
B contém A
U
B
A é subconjunto de B
c
d A a
A está contido em B
b
e
C = { 5, 6, 3, 2 }
B contém A
D = { 3, 5, 7, 6 }
C não é subconjunto de D
C não está contido em D
Prof: Alexsandro de Sousa
Conjunto das Partes:
Chamamos de conjunto das Partes do conjunto A e representamos por
P(A), o conjunto de todos os subconjuntos do conjunto A.
Escrever todos os subconjuntos do conjunto A = {0, 5, 7, 9}.
-Subconjunto com nenhum elemento:
-Subconjuntos com um elemento: {0}; {5}; {7}; {9}
-Subconjuntos com dois elementos: {0,5}; {0,7}; {0,9}; {5,7}; {5,9}; {7;9}
-Subconjuntos com três elementos: {0,5,7}; {0,5,9}; {0,7,9}; {5,7,9}
-Subconjuntos com quatro elementos: {0,5,7,9}
O número total de subconjuntos é igual a 16.
Prof: Alexsandro de Sousa
União:
Dados dois conjuntos A e B chama-se união (ou reunião) entre A e B ao
conjunto formado pelos elementos de A ou B.
A B {x x A ou x B}
Exemplo:
A {0, 2, 4, 6, 7, 8}
B {3, 4, 6, 9}
A B {0, 2, 3, 4, 6, 7, 8, 9}
Prof: Alexsandro de Sousa
Diagramas de Venn representativos da união entre A e B.
B A logo , A B A
Prof: Alexsandro de Sousa
A B logo , A B B
Intersecção:
Dados dois conjuntos A e B chama-se intersecção entre A e B ao conjunto
formado pelos elementos comuns entre A e B, isto é, pelos elementos que
Pertencem ao conjunto A e ao conjunto B.
A B {x x A e x B}
Exemplo:
A {0, 2, 4, 6, 7, 8}
B {3, 4, 6, 9}
A B {4, 6}
Prof: Alexsandro de Sousa
Diagramas de Venn representativos da intersecção entre A e B.
B A logo , A B B
Prof: Alexsandro de Sousa
A B logo , A B A
Diferença:
Dados dois conjuntos A e B chama-se diferença entre A e B ao conjunto
formado pelos elementos do conjunto A que não pertencem ao conjunto
B.
A B {x x A e x B}
B A {x x B e x A}
Exemplo:
A {0, 2, 4, 6, 7, 8}
B {3, 4, 6, 9}
A B {0, 2, 7, 8}
Prof: Alexsandro de Sousa
B A {3, 9}
Diagramas de Venn representativos de A - B.
A B log o, A B
Diagramas de Venn representativos de B - A.
B A log o, B A
Prof: Alexsandro de Sousa
MATEMÁTICA
Complementar:
Prof. Alexsandro de Sousa
Sejam dois conjuntos A e B tais que B A, chama se complementar de B em relação a A
ao conunto A B.
C A B, se B A
B
A
Exemplo:
A {0, 2, 4, 6, 7, 8}
B { 4, 6, 7}
C AB A B {0, 2, 8}
Prof: Alexsandro de Sousa
Prof. Alexsandro de Sousa
B
Diagrama de Venn para C A
Prof: Alexsandro de Sousa
MATEMÁTICA
Prof. Alexsandro de Sousa
Problemas Envolvendo Conjuntos.
Exemplos:
As provas de recuperação em matemática e física de uma escola
foram feitas no mesmo dia e durante a prova, observou-se a presença de 42 alunos. Sabendo-se que 25 alunos fizeram a prova
de matemática e 32 fizeram a de física, determine:
a) O número de alunos que fizeram as duas provas;
b) O número de alunos que fizeram apenas a prova de matemática;
c) O número de alunos que fizeram apenas a prova de física.
Prof: Alexsandro de Sousa
Numa pesquisa sobre a qualidade dos serviços oferecidos pelas
Prof. Alexsandro de Sousa
MATEMÁTICA
empresas
de fornecimento de água (A), energia elétrica (E) e TV por
assinatura (T) de um bairro, obteve-se um grande número de
reclamações. A tabela a seguir expressa o número de reclamações de
300 entrevistados durante a pesquisa.
Com base na tabela, determine:
a) O número de pessoas que não reclamaram de nenhum serviço;
b) O número de entrevistados que reclamaram apenas do serviço oferecido
pela empresa de fornecimento de água;
c) O número de entrevistados que reclamaram de apenas um serviço;
d) O número de entrevistados que reclamaram de pelo menos dois serviços.
Prof: Alexsandro de Sousa